•  Анализ финансовых данных
•  Банковское дело
•  Бухгалтерский учёт
•  Деньги Банки Кредит
•  Дэй Трейдинг
•  Долгосрочное инвестирование
•  Корпоративные финансы
•  Макроэкономика
•  Макроэкономический анализ
•  Микроэкономика
•  Налоги и налогообложение
•  Оценка финансовых активов
•  Скальпинг
•  Теория Игр
•  Торговые стратегии
•  Учебник по CSS
•  Учебник по HTML
•  Учебник по PHP
•  Учебник по PYTHON
•  Финансовая математика
•  Финансовые рынки
•  Финансовый менеджмент
•  Финансы
•  Эконометрика
•  Экономическая статистика
•  Экономический анализ

ЗАДАЧА №1

Условия задачи:

В отделе 20 сотрудников, каждый из которых по списку имеет свой порядковый номер от 1 до 20. Руководитель отдела решил поощрить сотрудников, вручив каждому с четным номером – денежную премию, с номером, который делится на 3 – сертификат на пребывание в спа-отеле, а остальным оплатил краткосрочные языковые курсы.

Какова вероятность того, что сотрудник получил:

а) два вознаграждения;

б) ровно одно вознаграждение?

  Пункт «а»:

Вероятность вручения премии сотрудникам с четными номерами:

Р1 = 10/20

Вероятность вручения сертификата: Р2=6/20=3/10.

Вероятность получения курсов: Р3=7/20.

Вероятность получения двух вознаграждений это пересечение P1 и Р2:

Р12=(10/20)*(3/10) = 3/20

  Пункт «б»:

Из условия задачи мы знаем, что вознаграждение получили все 20 сотрудников, а так же из решения пункта задачи «а», мы определили вероятность получения двух вознаграждений, поэтому для того чтобы найти вероятность получения ровно одного вознаграждения, мы можем из 100% вероятности вычесть вероятность получения двух вознаграждений:

Р123=1- 3/20 = 17/20.

ОТВЕТ:

  а) 3/20,

  б) 17/20.

ЗАДАЧА №2

Условия задачи:

В магазин поступили телевизоры от трех дистрибьютеров в отношении 1:3:6. Телевизоры, поступающие от 1-го дистрибьютора, требуют наладки в 3% случаев, от 2-го и 3-го – соответственно 2% и 1%. Найти вероятность того, что поступивший в магазин телевизор требует наладки.

Исходя из условия задачи, найдем соотношение партий телевизоров поступающих от трех дистрибьютеров: всего 1+3+6 = 10 частей товара, значит: для первого дистрибьютера 1/10 = 0,1 товара, для второго 3/10 = 0,3 товара, и для третьего 6/10 = 0,6 товара. Теперь, вероятность того, что поступивший телевизор будет требовать наладки можно найти по формуле полной вероятности: 0,1*0,03+0,3*0,02+0,6*0,01 = 0,003+0,006+0,006 = 0,015.

ОТВЕТ:

  0,015.

ЗАДАЧА №3

Условия задачи:

Фирма взяла 5 машин в лизинг. Известно, что вероятность того, что машина попадет в аварию за время действия договора, равна 0,3.

Составить закон распределения случайной величины – числа аварий с данными машинами за время действия лизингового соглашения.

Найти ее математическое ожидание, дисперсию, среднее квадратическое отклонение, построить функцию распределения.

Для составления закона распределения случайной величины воспользуемся формулой Бернулли:

Пусть А - событие состоящее в том, что машина попадет в аварию. Вероятность наступления события А для каждой машины постоянна и равна р=0,3, и таким образом вероятность того, что машина не попадет в аварию равна q = 1-p = 1-0,3 = 0,7.

Пусть $A_{\mathrm{k,5}}$ – событие состоящее в том, что количество k машин из 5 (по условию) попадет в аварию (k = 0, 1, 2, 3, 4 или 5).

• Для составления закона распределения случайной величины воспользуемся формулой Бернулли для каждого k:
  
  $P\left(A_{\mathrm{0,5}}\right)=P_{\mathrm{0,5}}=P_5\left(0\right)=C_5^0*p^0*q^{\mathrm{5-0}}=\frac{5!}{0!*(5-0)!}*{\mathrm{0,3}}^0*{\mathrm{0,7}}^5=\mathrm{0,16807}$
  
  $P\left(A_{\mathrm{1,5}}\right)=P_{\mathrm{1,5}}=P_5\left(1\right)=C_5^1*p^1*q^{\mathrm{5-1}}=\frac{5!}{1!*(5-1)!}*{\mathrm{0,3}}^1*{\mathrm{0,7}}^4=\mathrm{0,36015}$
  
  $P\left(A_{\mathrm{2,5}}\right)=P_{\mathrm{2,5}}=P_5\left(2\right)=C_5^2*p^2*q^{\mathrm{5-2}}=\frac{5!}{2!*(5-2)!}*{\mathrm{0,3}}^2*{\mathrm{0,7}}^3=\mathrm{0,3087}$
  
  $P\left(A_{\mathrm{3,5}}\right)=P_{\mathrm{3,5}}=P_5\left(3\right)=C_5^3*p^3*q^{\mathrm{5-3}}=\frac{5!}{3!*(5-3)!}*{\mathrm{0,3}}^3*{\mathrm{0,7}}^2=\mathrm{0,1323}$
  
  $P\left(A_{\mathrm{4,5}}\right)=P_{\mathrm{4,5}}=P_5\left(4\right)=C_5^4*p^4*q^{\mathrm{5-4}}=\frac{5!}{4!*(5-4)!}*{\mathrm{0,3}}^4*{\mathrm{0,7}}^1=\mathrm{0,0.02835}$
  
  $P\left(A_{\mathrm{5,5}}\right)=P_{\mathrm{5,5}}=P_5\left(5\right)=C_5^5*p^5*q^{\mathrm{5-5}}=\frac{5!}{5!*(5-5)!}*{\mathrm{0,3}}^5*{\mathrm{0,7}}^0=\mathrm{0,00243}$
  

• Составим закон распределения случайной величины – числа аварий с данными машинами за время действия лизингового соглашения:

  
  

  x	0	1	2	3	4	5
  p	0.16807	0.36015	0.3087	0.1323	0.02835	0.00243

  
  
  

  Где х – количество машин попавших в аварию, p – вероятность того, что данное кол-во машин попадет в аварию.

  Проверим выполнение основного свойства закона распределения:

  0,16807 + 0,36015 + 0,3087 + 0,1323 + 0,02835 + 0,00243 = 1.

• Найдем математическое ожидание $M(\xi ):$
  
  $M\xi ={\sum }_{\mathrm{i=1}}^n{x}_i{p}_i=0*\mathrm{0,16807}+1*\mathrm{0,36015}+2*\mathrm{0,3087}+3*\mathrm{0,01323}+4*\mathrm{0,02835}+5*\mathrm{0,00243}=\mathrm{1,5}$

• Для вычисления дисперсии воспользуемся свойством дисперсии:

  $D\xi =M{\xi }^2-M^2\xi$

  Таким образом, необходимо найти математическое ожидание квадрата случайной величины $M{\xi }^2$, которое определяем по формуле:

  $M{\xi }^2={\sum }_{\mathrm{i=1}}^n{x}_i^2{p}_i=0^2*\mathrm{0,16801}+1^2*\mathrm{0,36015}+2^2*\mathrm{0,3087}+3^2*\mathrm{0,1323}+4^2*\mathrm{0,02835}+5^2*\mathrm{0,00243}=\mathrm{3,3}$
  

  Тогда

  $D\xi =M{\xi }^2-M^2\xi =\mathrm{3,3}-{\mathrm{1,5}}^2=\mathrm{1,05}$
  

• Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии, т.е.:

  ${\sigma }_{\xi }=\sqrt{D\xi }=\sqrt{\mathrm{1,05}}\approx \mathrm{1,025}$
  

• Построим функцию распределения:

  $\{\begin{array}{c}0\mathrm{при}x\le 0\\ \mathrm{0,16807}\mathrm{при}0<x\le 1\\ \mathrm{0,52822}\mathrm{при}1<x\le 2\\ \mathrm{0,83692}\mathrm{при}2<x\le 3\\ \mathrm{0,96922}\mathrm{при}3<x\le 4\\ \mathrm{0,99757}\mathrm{при}4<x\le 5\\ 1\mathrm{при}x>5\end{array}$

• Построим график функции распределения:

  

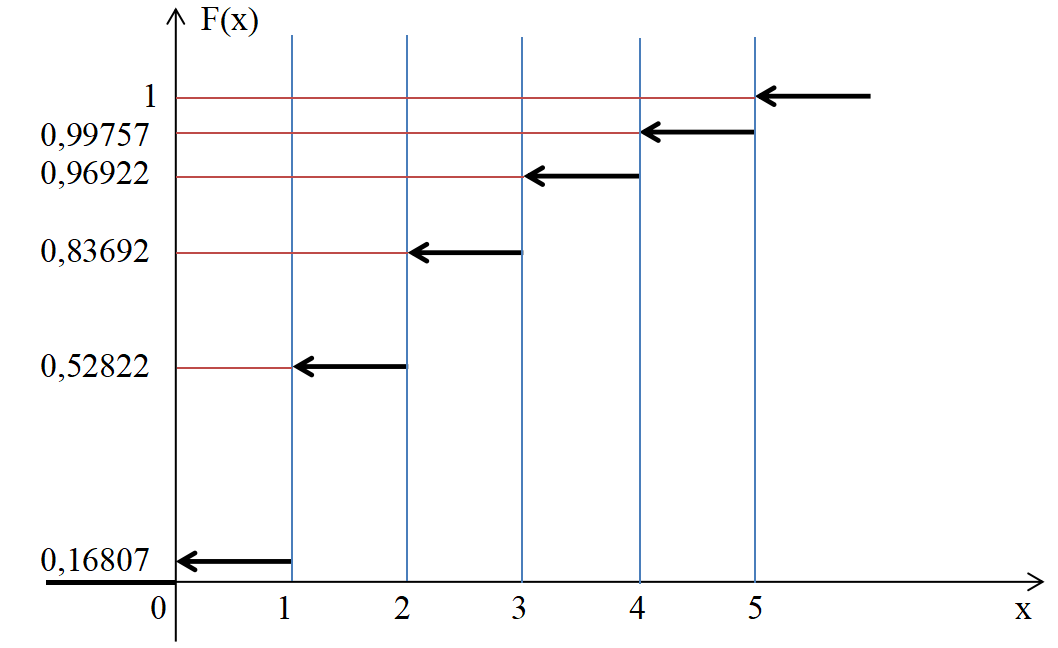
ОТВЕТ:

1) Закон распределения случайной величины – числа аварий с данными машинами за время действия лизингового соглашения:

Где х – количество машин попавших в аварию, p – вероятность того, что данное кол-во машин попадет в аварию.

2) Математическое ожидание $M(\xi ):$

3) Дисперсия $D(\xi )$ :

4) Среднее квадратическое отклонение ${\sigma }_{\xi }$:

5) Функция распределения:

ЗАДАЧА №4

Условия задачи:

$\xi$ и $\eta$ распределено по геометрическому закону с параметром p=0,2 и р=0,1 соответственно, то есть вероятности вычисляются по формуле $Р(\xi =k)=q^{\mathrm{k-1}}*p={\mathrm{0,8}}^{\mathrm{k-1}}*\mathrm{0,2},\mathrm{ где }k=1,2,3,\dots .\mathrm{ \; и }Р(\eta =k)=q^{\mathrm{k-1}}*p={\mathrm{0,9}}^{\mathrm{k-1}}*\mathrm{0,1},\mathrm{ \; где }k=1,2,3,\dots .$

ОТВЕТ: математическое ожидание величины $\gamma =\xi -2\eta$:   $M(\xi -2\eta )=-15$, дисперсия величины $\gamma =\xi -2\eta$:   $D(\xi -2\eta )\approx \mathrm{244,236}$

ЗАДАЧА №5

Условия задачи:

• Выписать одномерные законы распределения случайных величин $\xi$ и $\eta$, вычислить математические ожидания М$\xi$, М$\eta$ и дисперсии D$\xi$, D$\eta$.
• Найти ковариацию Cov($\xi$,$\eta$) и коэффициент корреляции $\rho$($\xi$,$\eta$).
• Являются ли случайные события {$\eta$=2} и {$\xi$=4} зависимыми?
• Составить условный закон распределения случайной величины $\gamma =(\eta |\xi >5)$ и найти М$\gamma$ и D$\gamma$.

ОТВЕТ:

1) Законы распределения случайных величин $\xi$ и $\eta$:

Математические ожидания М$\xi$ , М$\eta$ и дисперсии D$\xi$ , D$\eta$:

М($\xi$) = 5,5;

D($\xi$) = 1,05;

М($\eta$) = 1,2;

D($\eta$) = 0,76.

2) Ковариация cov($\xi$,$\eta$) = -0,2.

Коэффициент корреляции $\rho$($\xi$,$\eta$) ≈ -0,105.

3) Случайные события {$\eta$=2} и {$\xi$=4} зависимыми не являются.

4) Условный закон распределения $\gamma$=($\eta$|$\xi$>5) имеет вид:

$M_{\gamma }=1$

$D_{\gamma }=\mathrm{0,8}$